Time-Series Analysis
Important Concepts, Handy Techniques, and Some Cautionary Tales
Superweek 2023
A travel tip…or Zoli as an unintentional travel agent?





Let’s think about time.
This presentation
40 minutes
Superweek
5 days

My last job
5 years

Yehoshua’s intros

“Time” is a tricky thing, but it’s at the core of what we do.

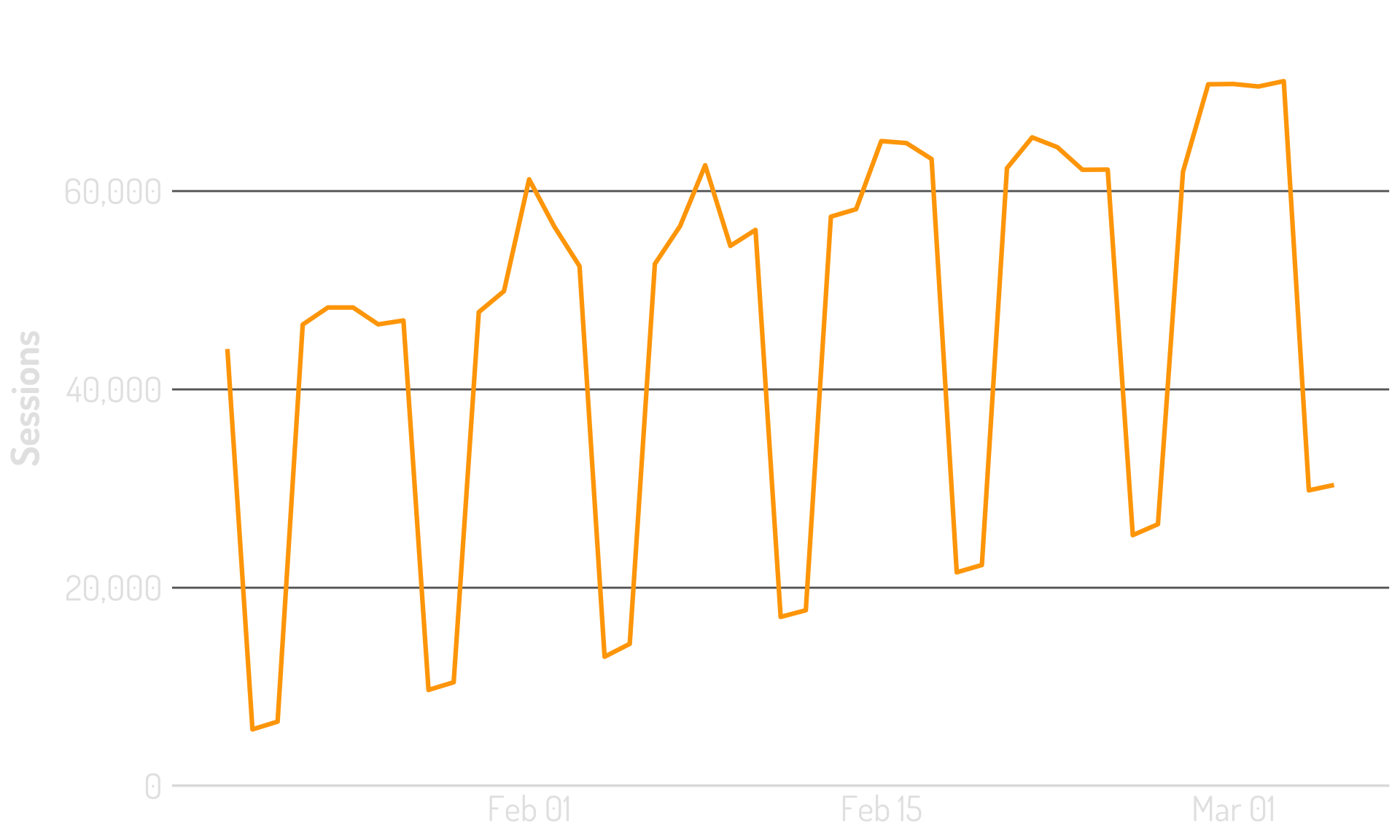
It rarely looks quite like this
It often has a weekly cycle to it

And it may have a trend to it

Let’s think about statistics
Statistics is all about estimating a population from a sample.
Our data exists over time.
So, what is our population?
Is it the past to the present?

Maybe. Maybe not.
Maybe it’s the past, present, and future?

Or…just the future?

But…we can’t sample from the future!
So…what is our sample?
Our sample is a sample timeframe.
This is imperfect.
Because our reality is constant change.
DALL-E 2: “A room full of puppies who all have different astonished expressions on their faces, digital art”
Time-series data is often
non-stationary.
A stationary time series is one whose statistical properties do not depend on the time at which the series is observed. 1
A stationary time series is one whose statistical properties do not depend on the time at which the series is observed. 1
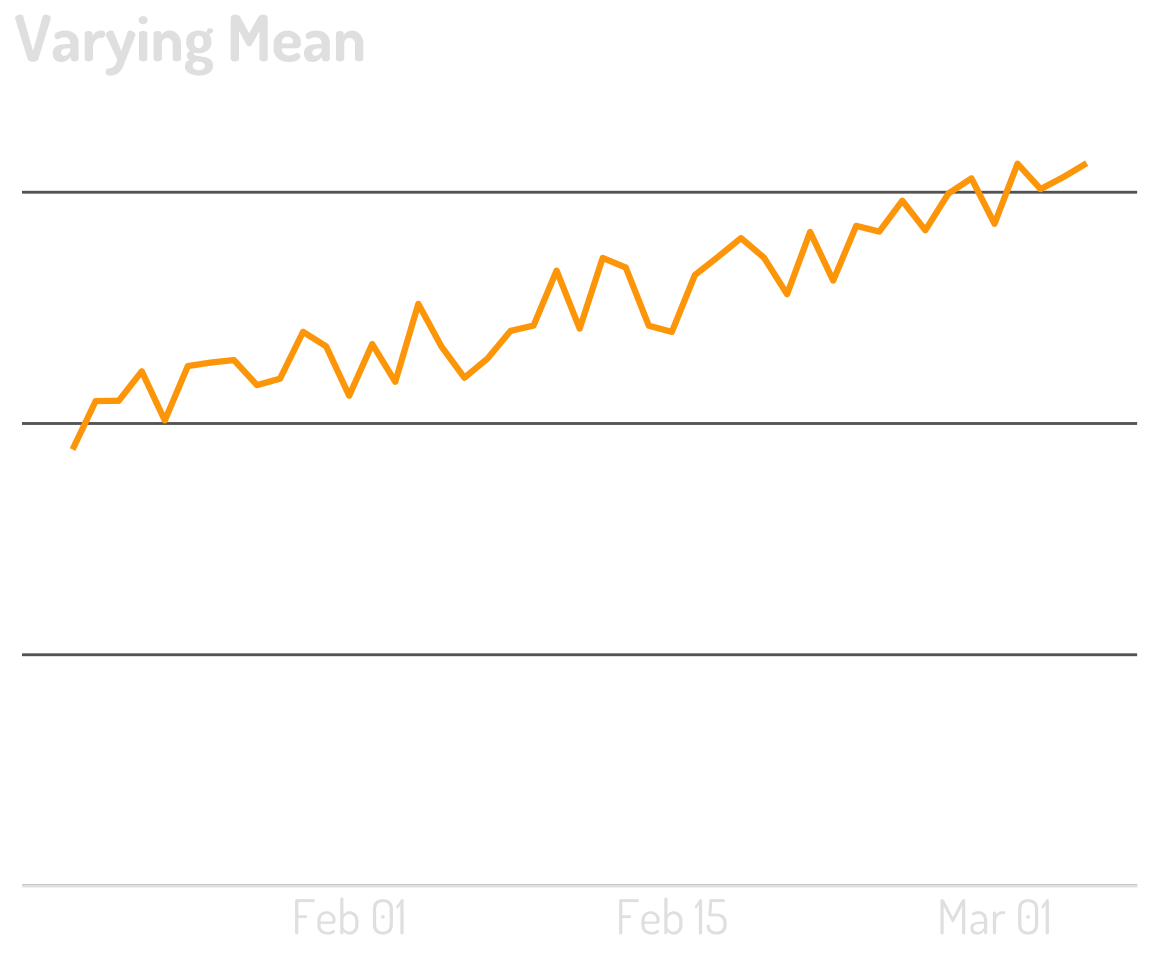
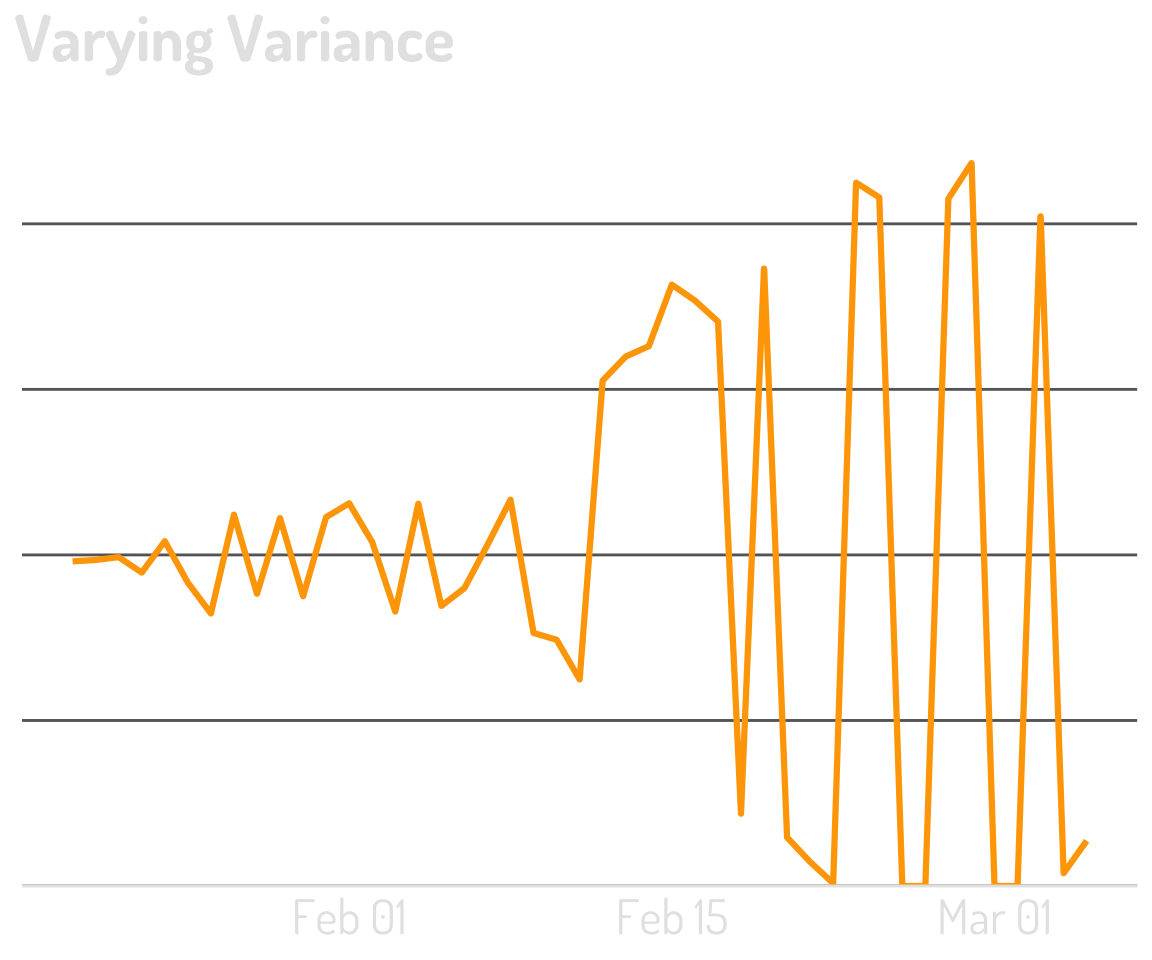
A stationary time series is one whose statistical properties do not depend on the time at which the series is observed. 1
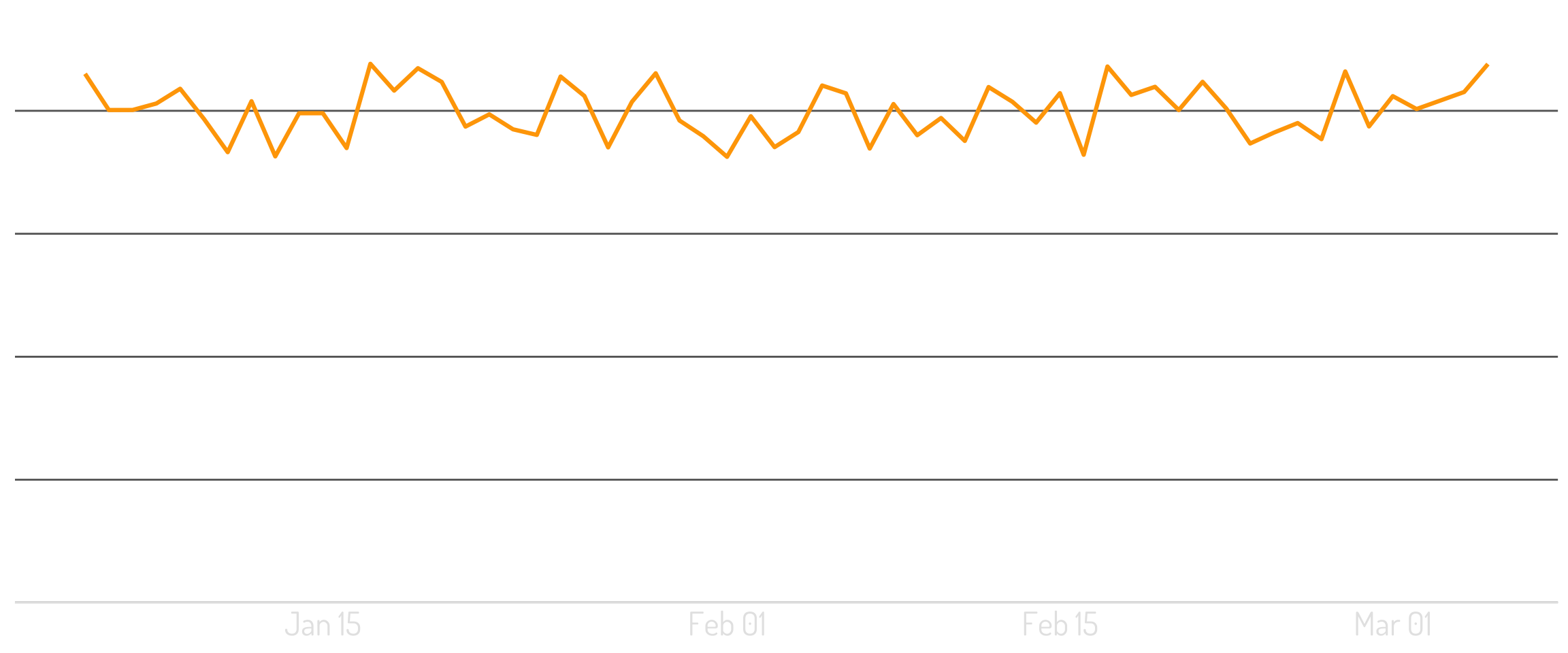
A stationary time series is one whose statistical properties do not depend on the time at which the series is observed. 1

One Antidote to Non-Stationarity: First Differences
Are these two metrics correlated?
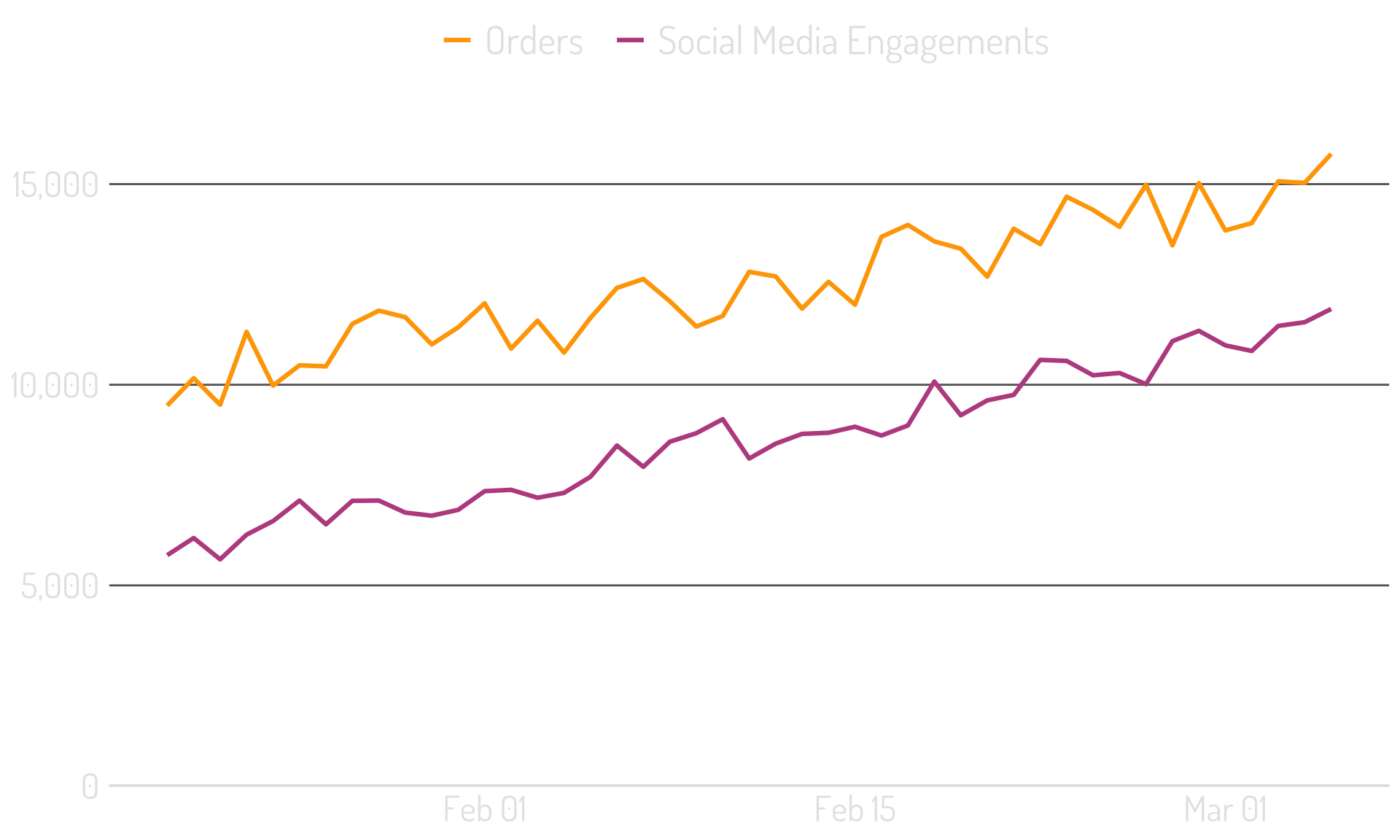
To the scatterplot!
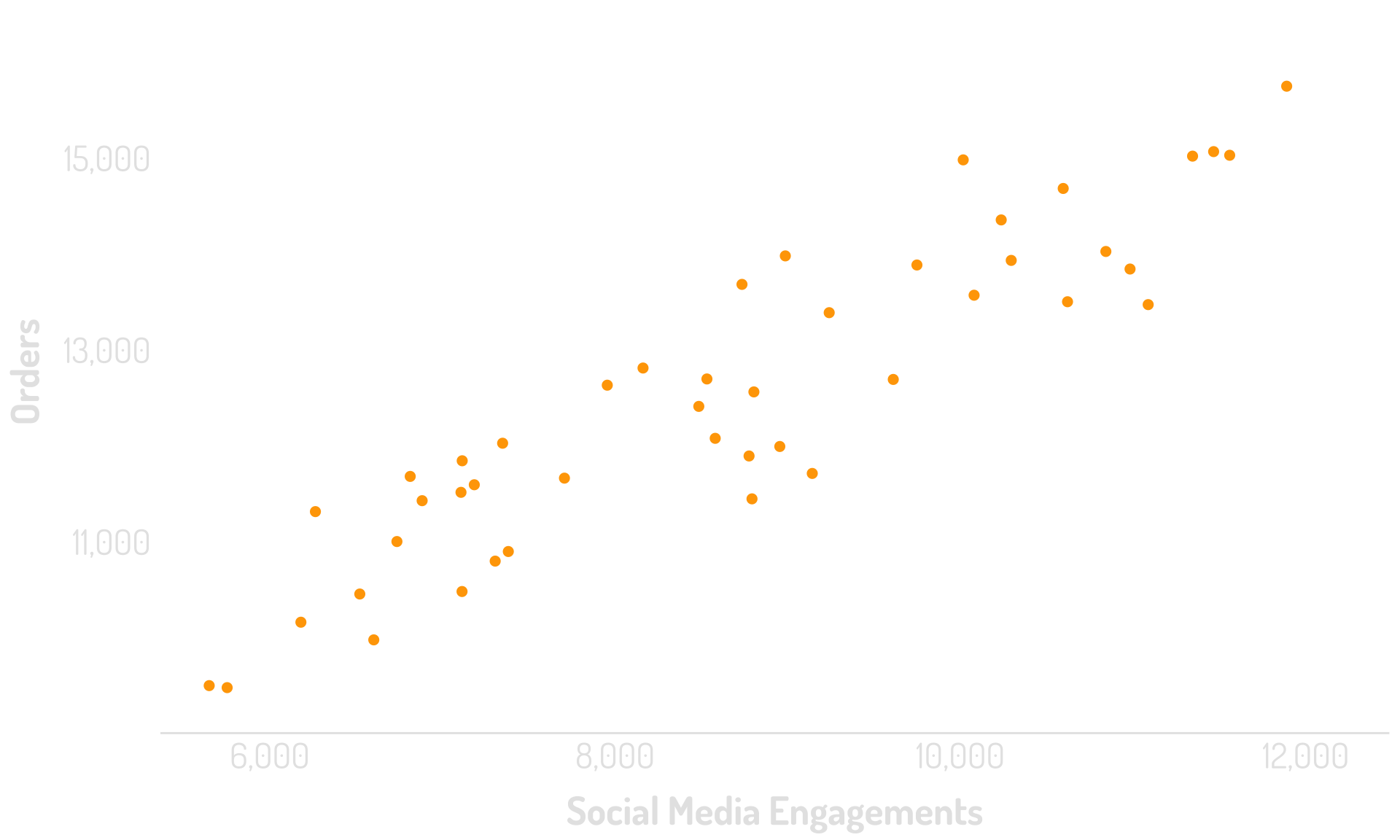
R2 = 0.84


If they’re correlated, then when one moves, the other will move similarly.
When one metric increases, the other should increase similarly.
When one metric decreases, the other should decrease similarly.
So, let’s look at the changes rather than the actual values.
This is called first differences.
| Date | Orders | 1st Diff: Orders |
|---|---|---|
| 2023-01-20 | 9,482 | |
| 2023-01-21 | 10,164 | |
| 2023-01-22 | 9,503 | |
| 2023-01-23 | 11,317 | |
| 2023-01-24 | 9,980 | |
| 2023-01-25 | 10,484 | |
| 2023-01-26 | 10,458 |
This is called first differences.
| Date | Orders | 1st Diff: Orders |
|---|---|---|
| 2023-01-20 | 9,482 | |
| 2023-01-21 | 10,164 | |
| 2023-01-22 | 9,503 | |
| 2023-01-23 | 11,317 | |
| 2023-01-24 | 9,980 | |
| 2023-01-25 | 10,484 | |
| 2023-01-26 | 10,458 |
This is called first differences.
| Date | Orders | 1st Diff: Orders |
|---|---|---|
| 2023-01-20 | 9,482 | |
| 2023-01-21 | 10,164 | |
| 2023-01-22 | 9,503 | |
| 2023-01-23 | 11,317 | 1,814 |
| 2023-01-24 | 9,980 | |
| 2023-01-25 | 10,484 | |
| 2023-01-26 | 10,458 |
This is called first differences.
| Date | Orders | 1st Diff: Orders |
|---|---|---|
| 2023-01-20 | 9,482 | NA |
| 2023-01-21 | 10,164 | 682 |
| 2023-01-22 | 9,503 | −661 |
| 2023-01-23 | 11,317 | 1,814 |
| 2023-01-24 | 9,980 | −1,337 |
| 2023-01-25 | 10,484 | 504 |
| 2023-01-26 | 10,458 | −26 |
From non-stationary to more stationary

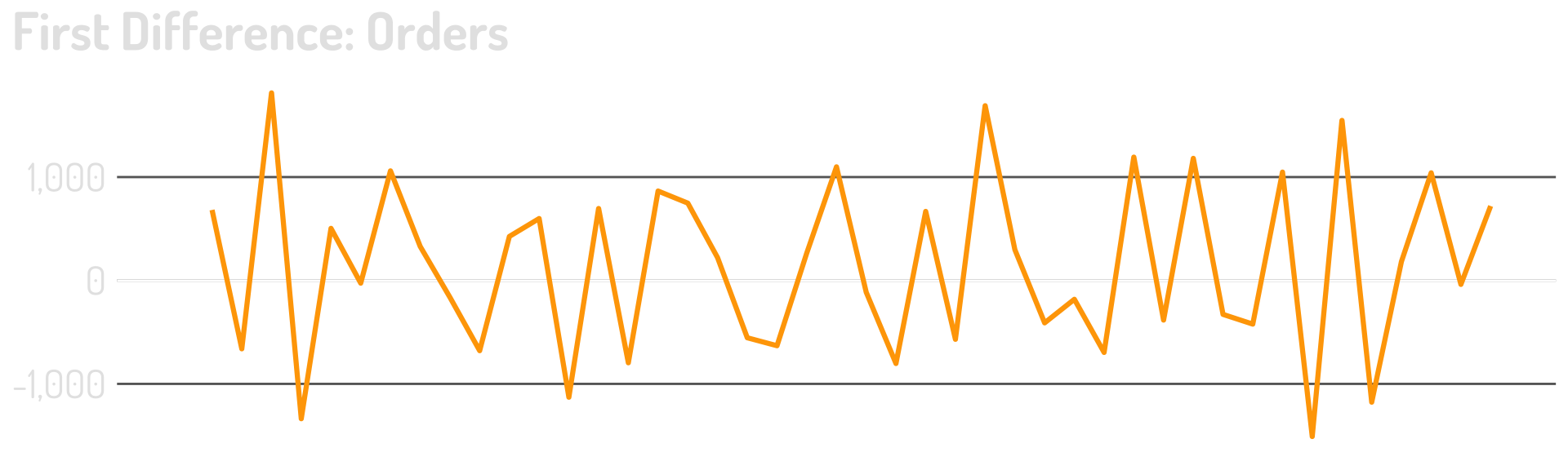
We can calculate first differences for both metrics
| Date | Orders | 1st Diff: Orders | Social | 1st Diff: Social |
|---|---|---|---|---|
| 2023-01-20 | 9,482 | NA | 5,754 | NA |
| 2023-01-21 | 10,164 | 682 | 6,181 | 427 |
| 2023-01-22 | 9,503 | −661 | 5,650 | −531 |
| 2023-01-23 | 11,317 | 1,814 | 6,265 | 615 |
| 2023-01-24 | 9,980 | −1,337 | 6,603 | 338 |
| 2023-01-25 | 10,484 | 504 | 7,114 | 511 |
| 2023-01-26 | 10,458 | −26 | 6,522 | −592 |
And then check the correlation!
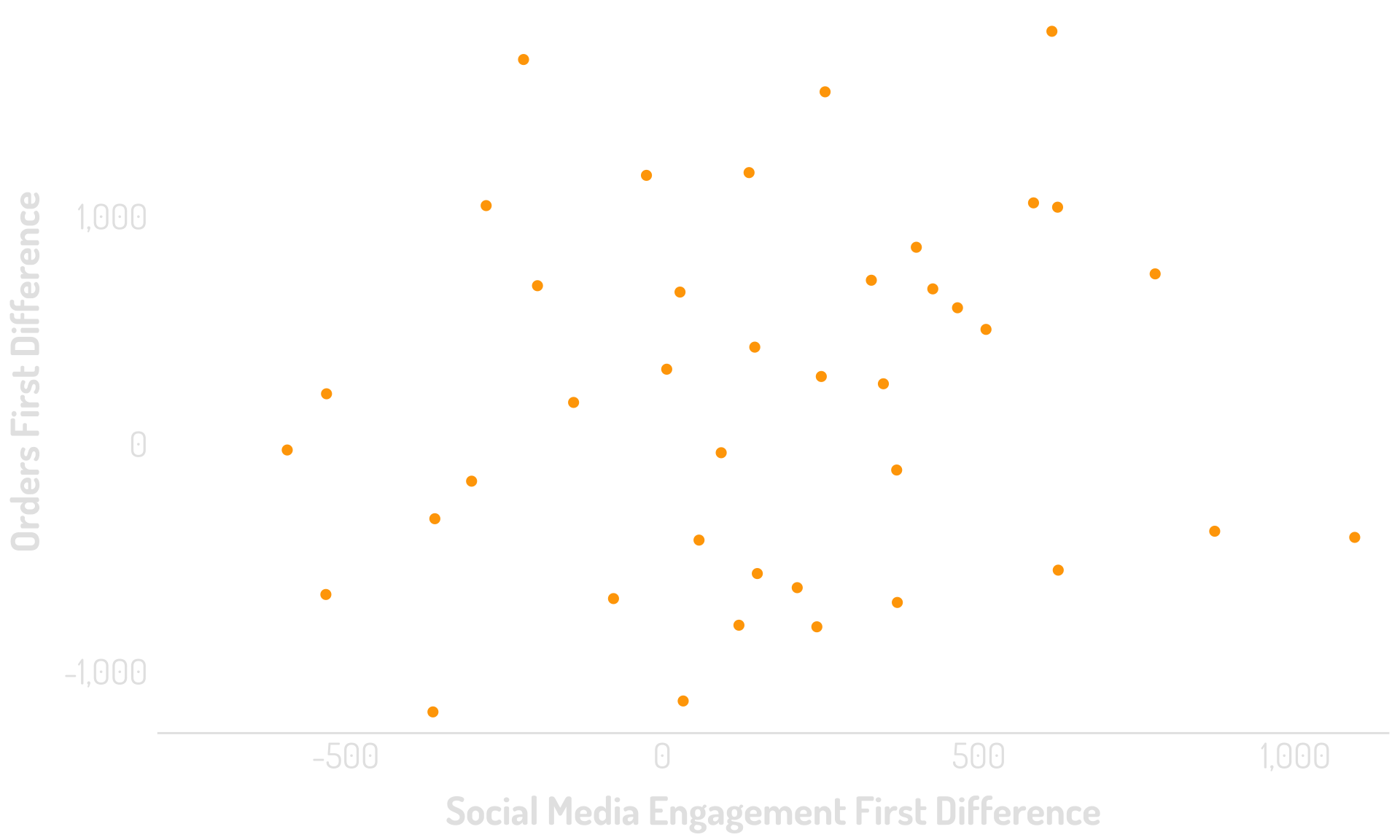
R2 = 0.00
These are both moving with time…but not directly with each other


Let’s shift gears

Decomposition can be amazing
Time-series decomposition, that is
A fairly “clean” series

The mean…is pretty meaningless
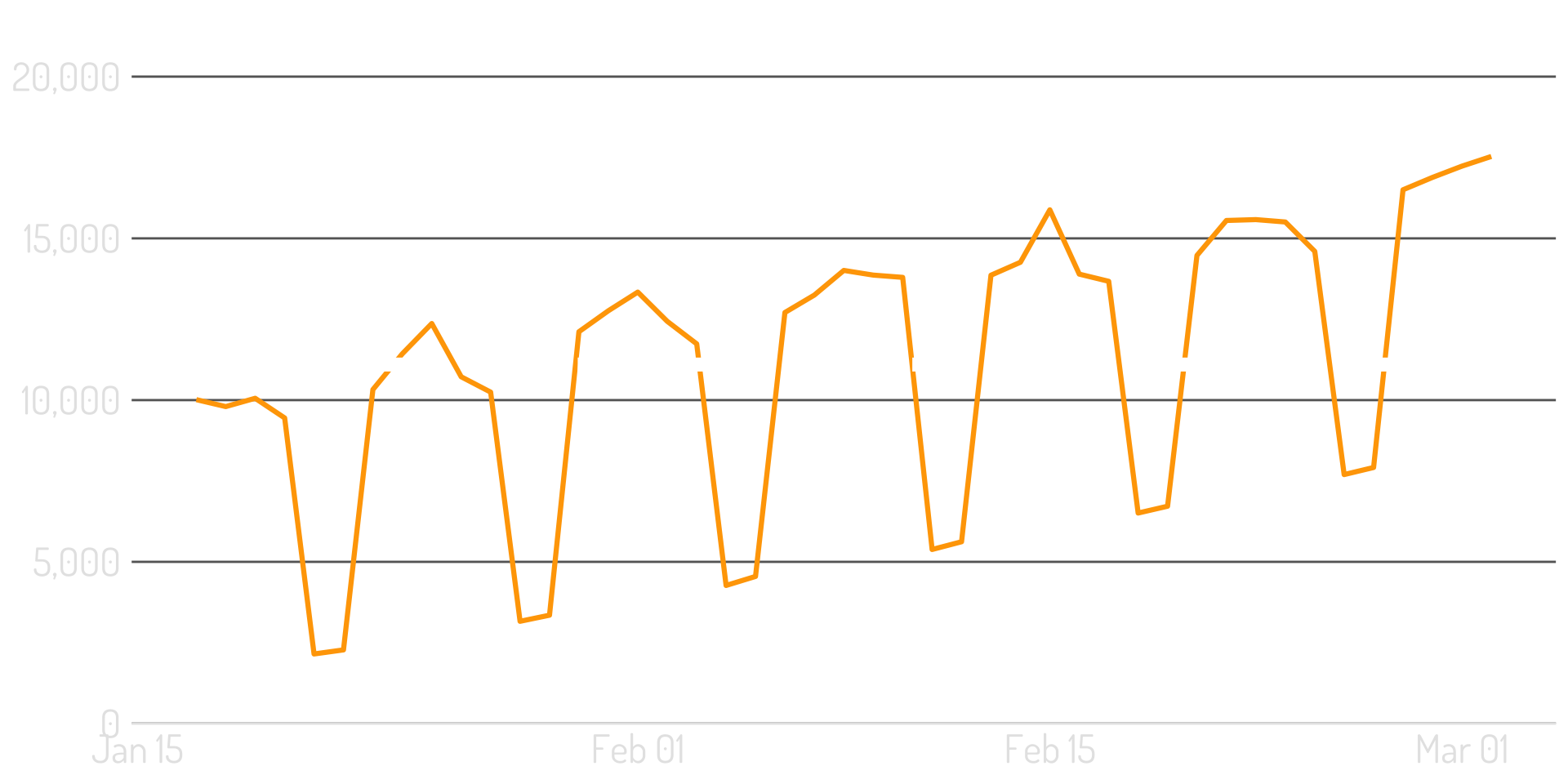
And so is the variance

Time-series decomposition does what our brain already wants to do
It “decomposes” the data into three components
It “decomposes” the data into three components


The Seasonal Component

The Trend Component

What’s Left!
“The Mean”
“The Variance”
Back to the overall series
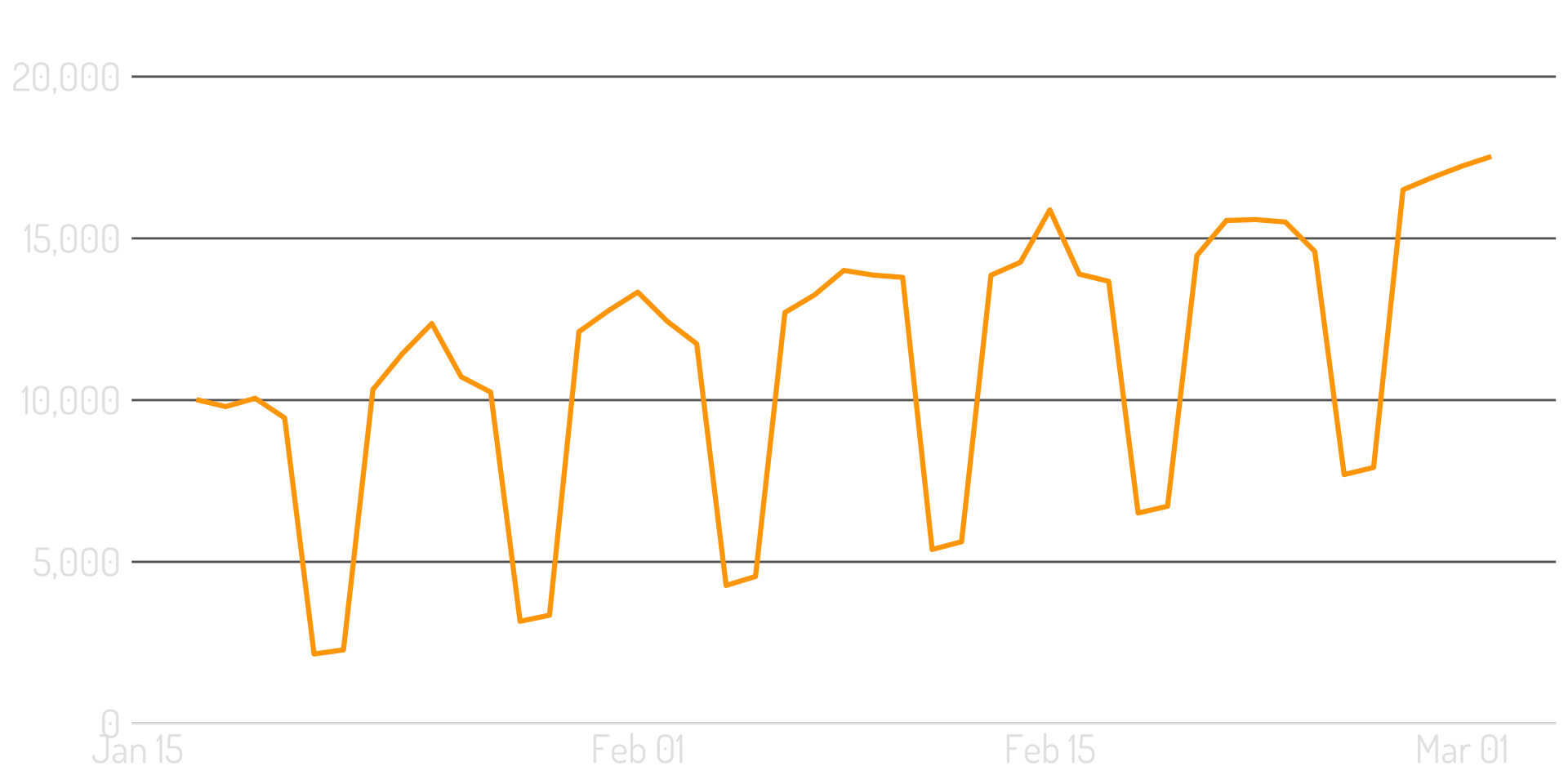
The original mean + variance…embarrassing?

Let’s try again
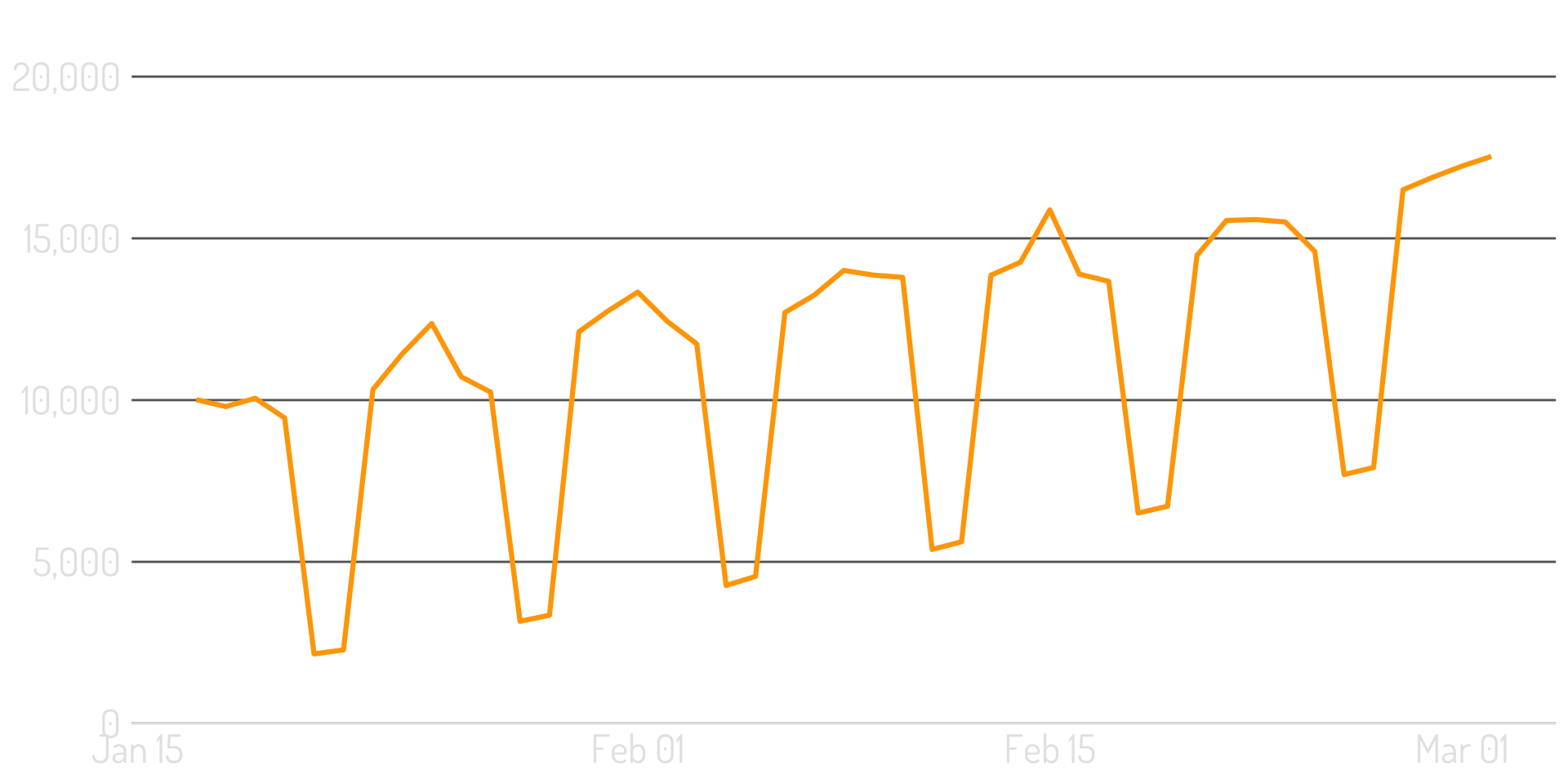
Seasonality + trend = the “mean”
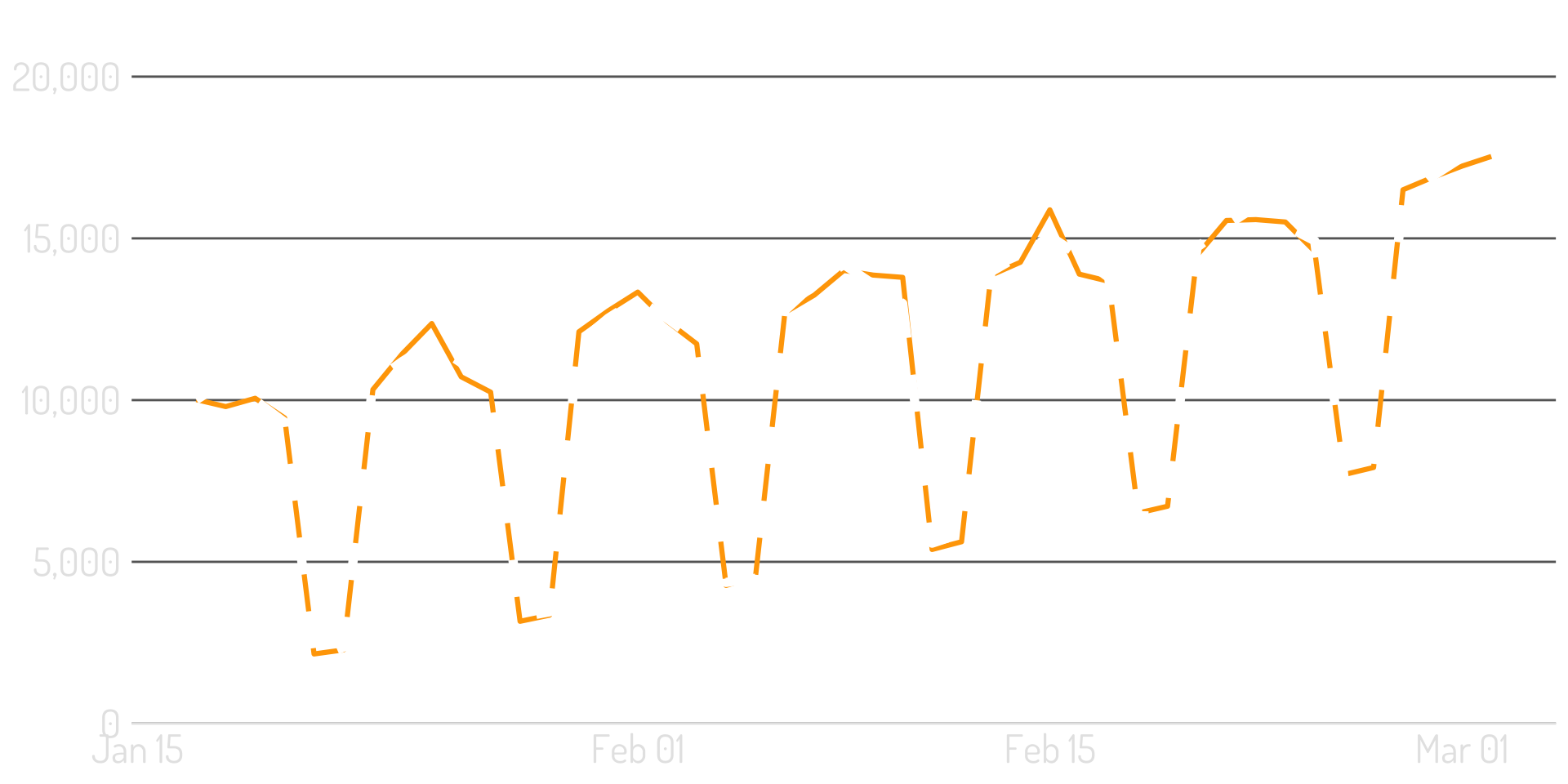
And the “variance” is just based on “what’s left”
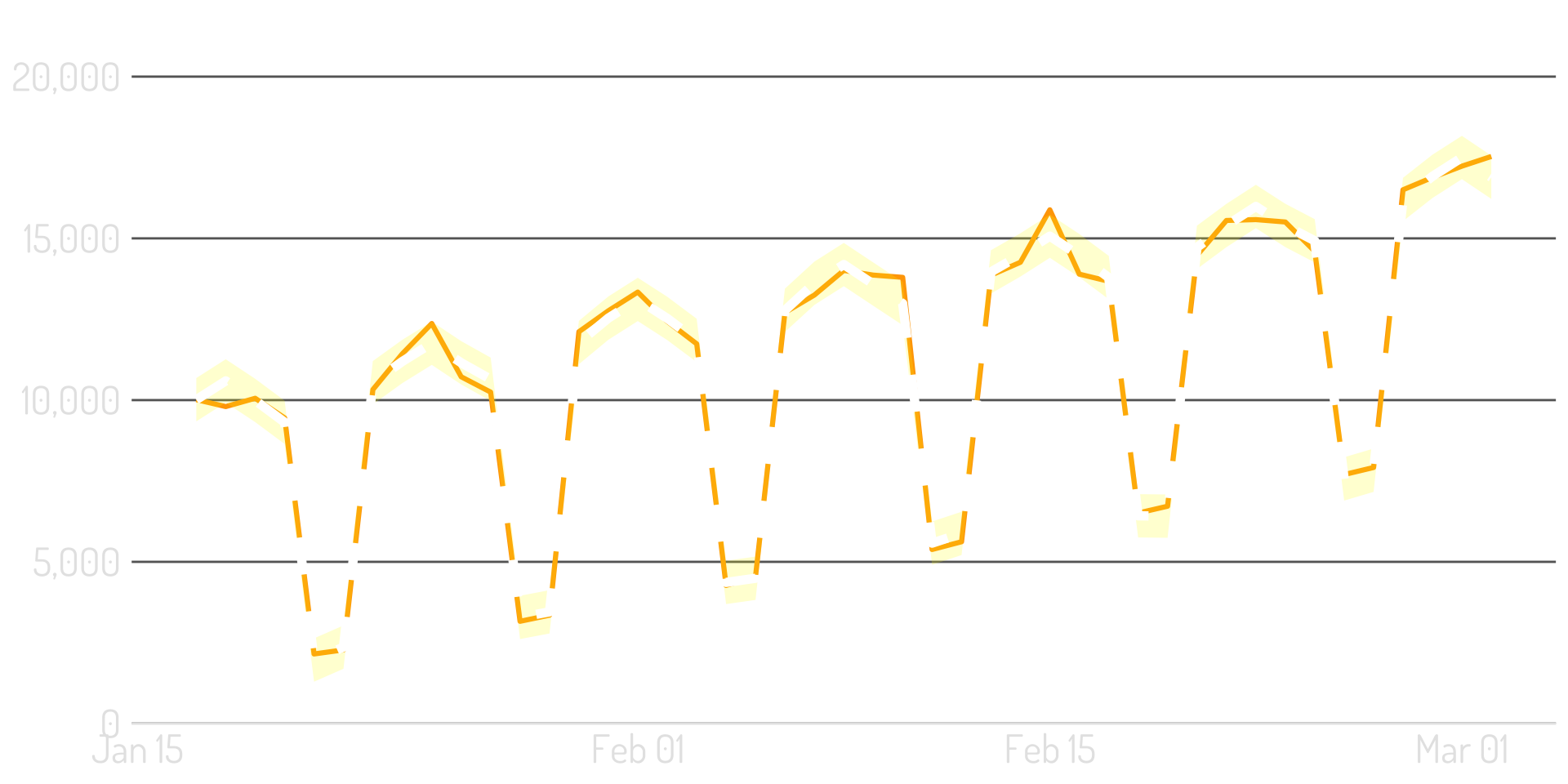

This is powerful!
(Loosely) it’s part of what’s happening with our next example.
And now…to Bayesian things!

Specifically, Bayesian Structural Time-Series

Time-series decomposition turned up to 11

Mark Edmondson built a tool using this 7 years ago!
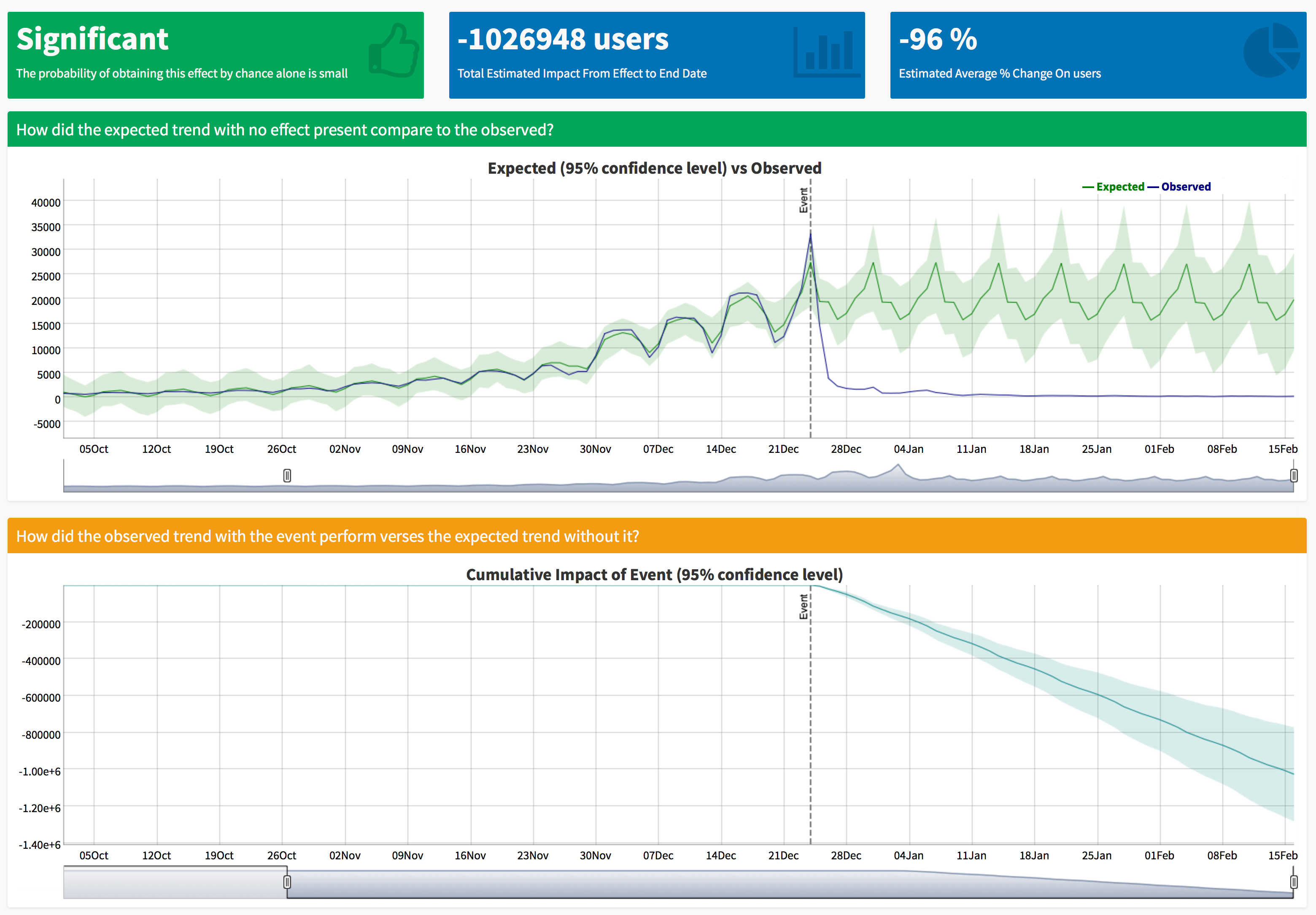
At its core: estimate the impact of an intervention

“We didn’t test it, so can we just do a pre-/post- analysis?”

What the marketer expects happened
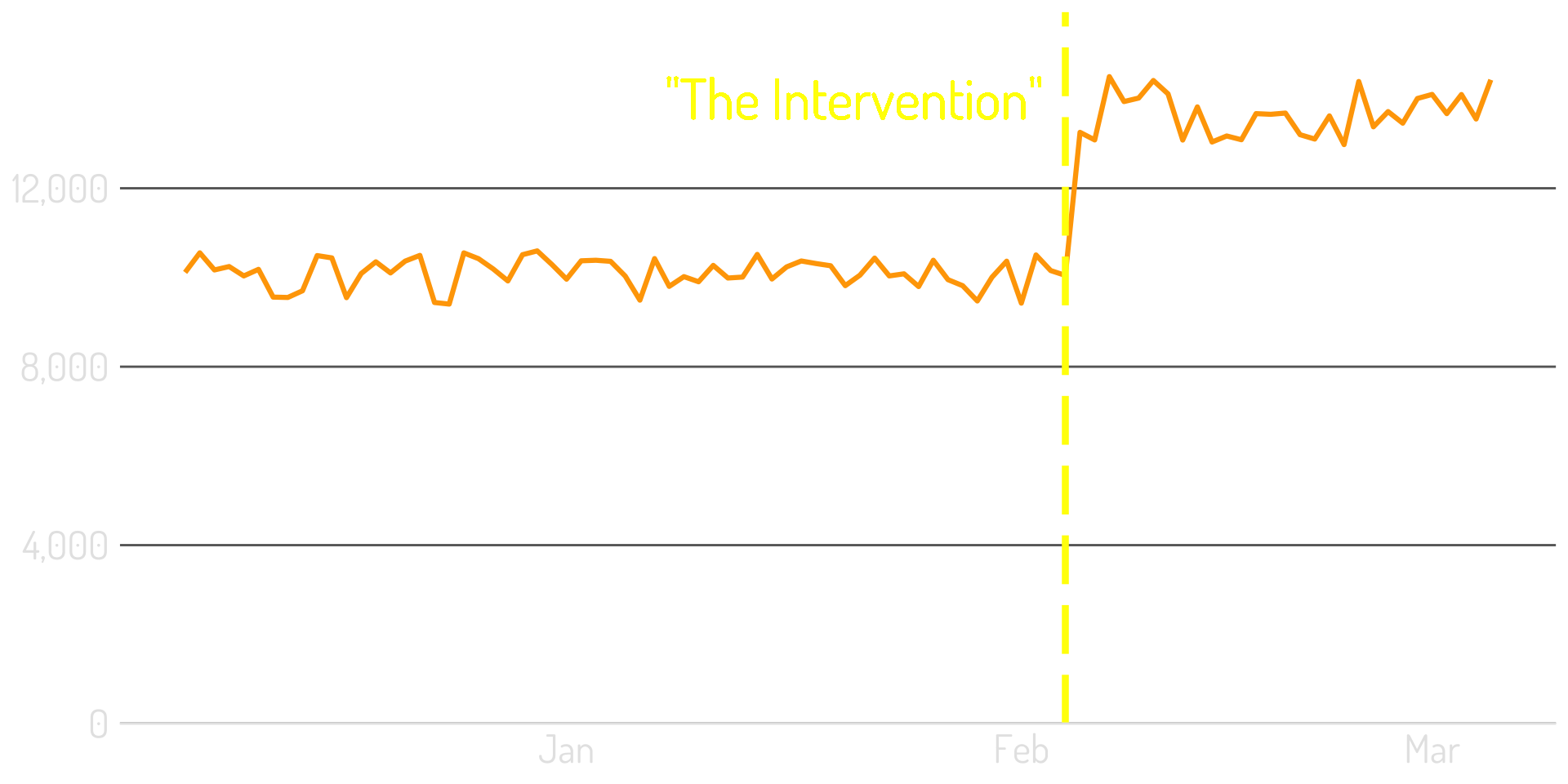
Typically, the change isn’t that big…
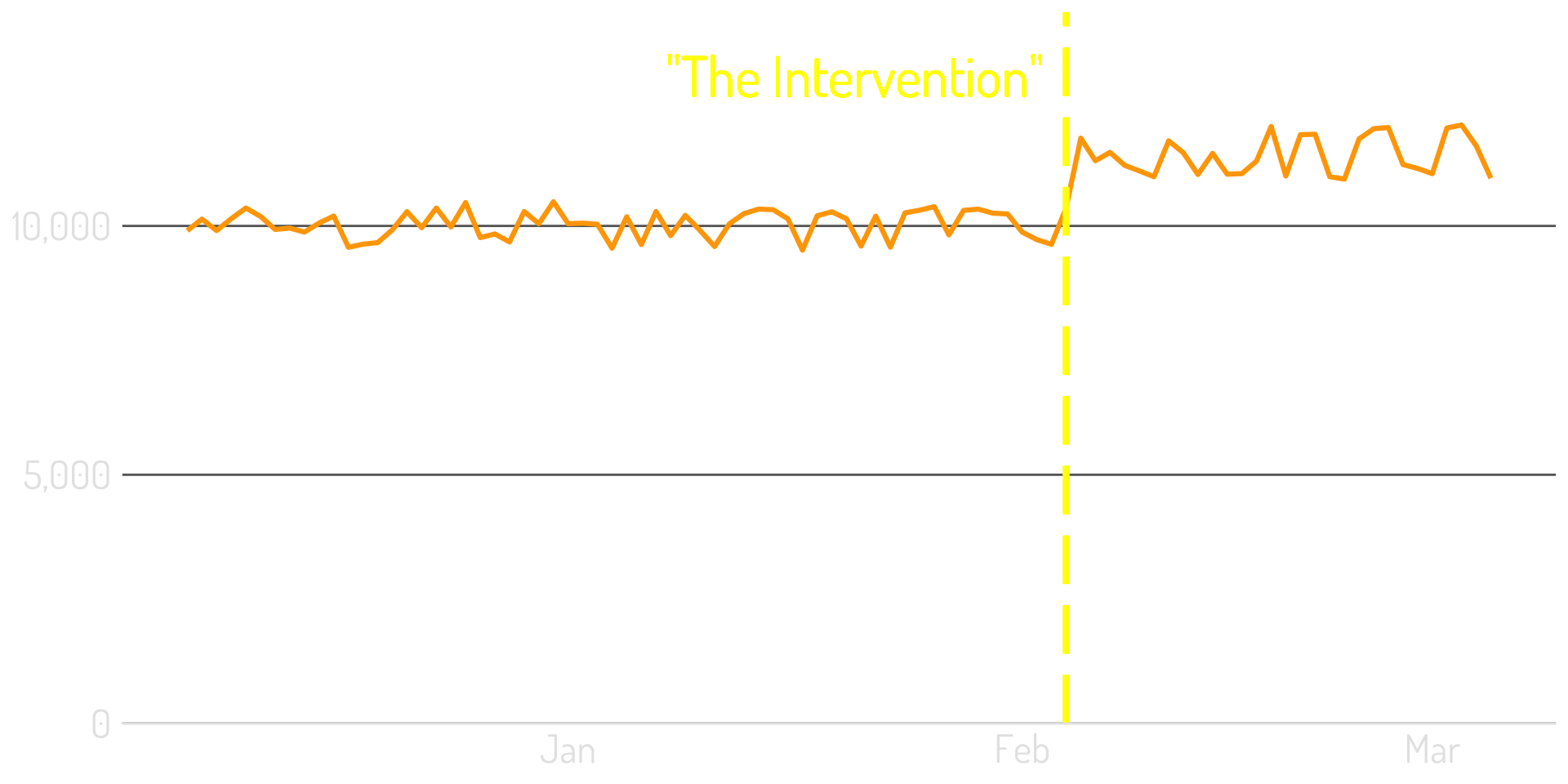
…and the data is a lot noisier…
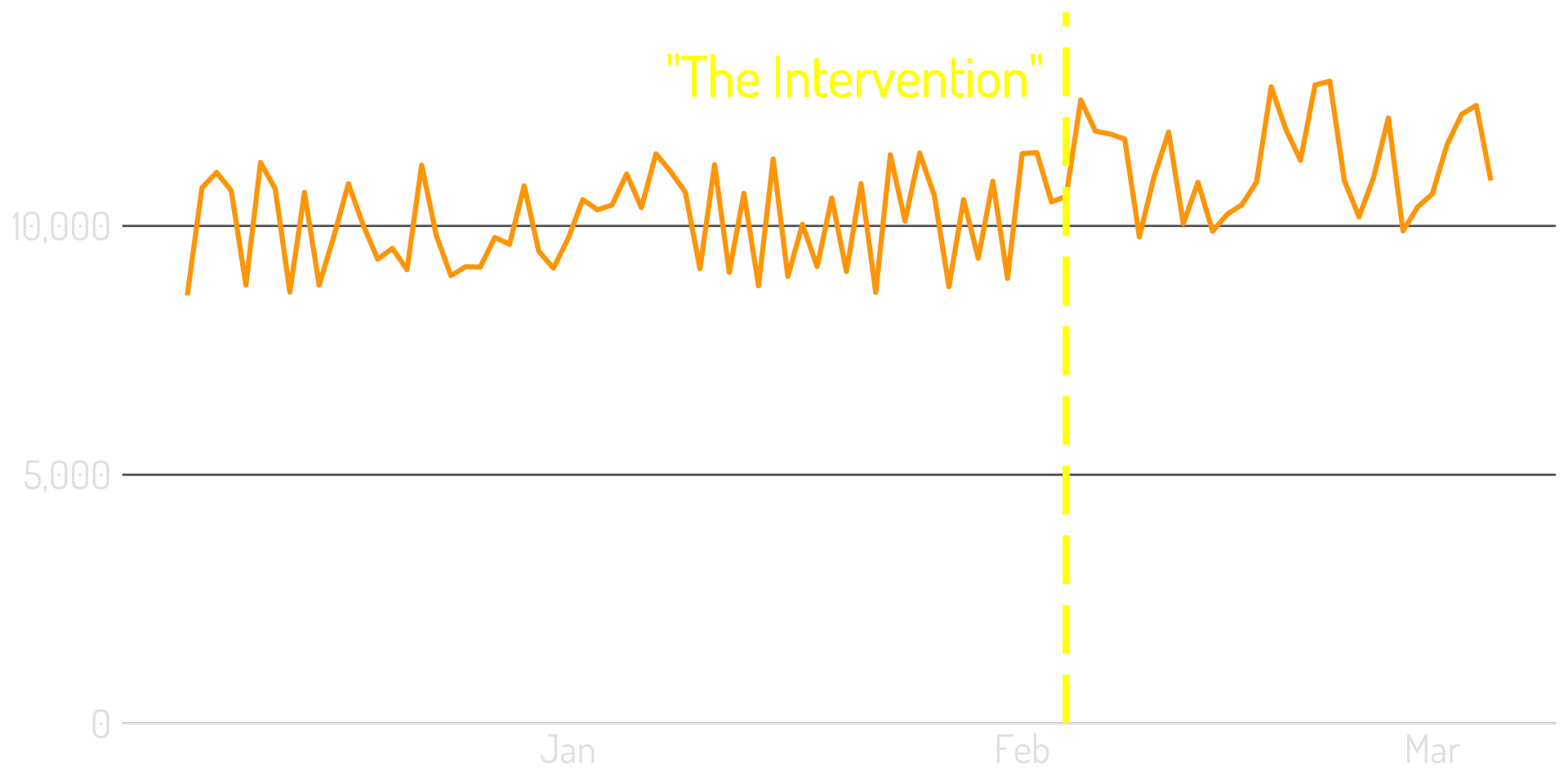
…and may have seasonality!
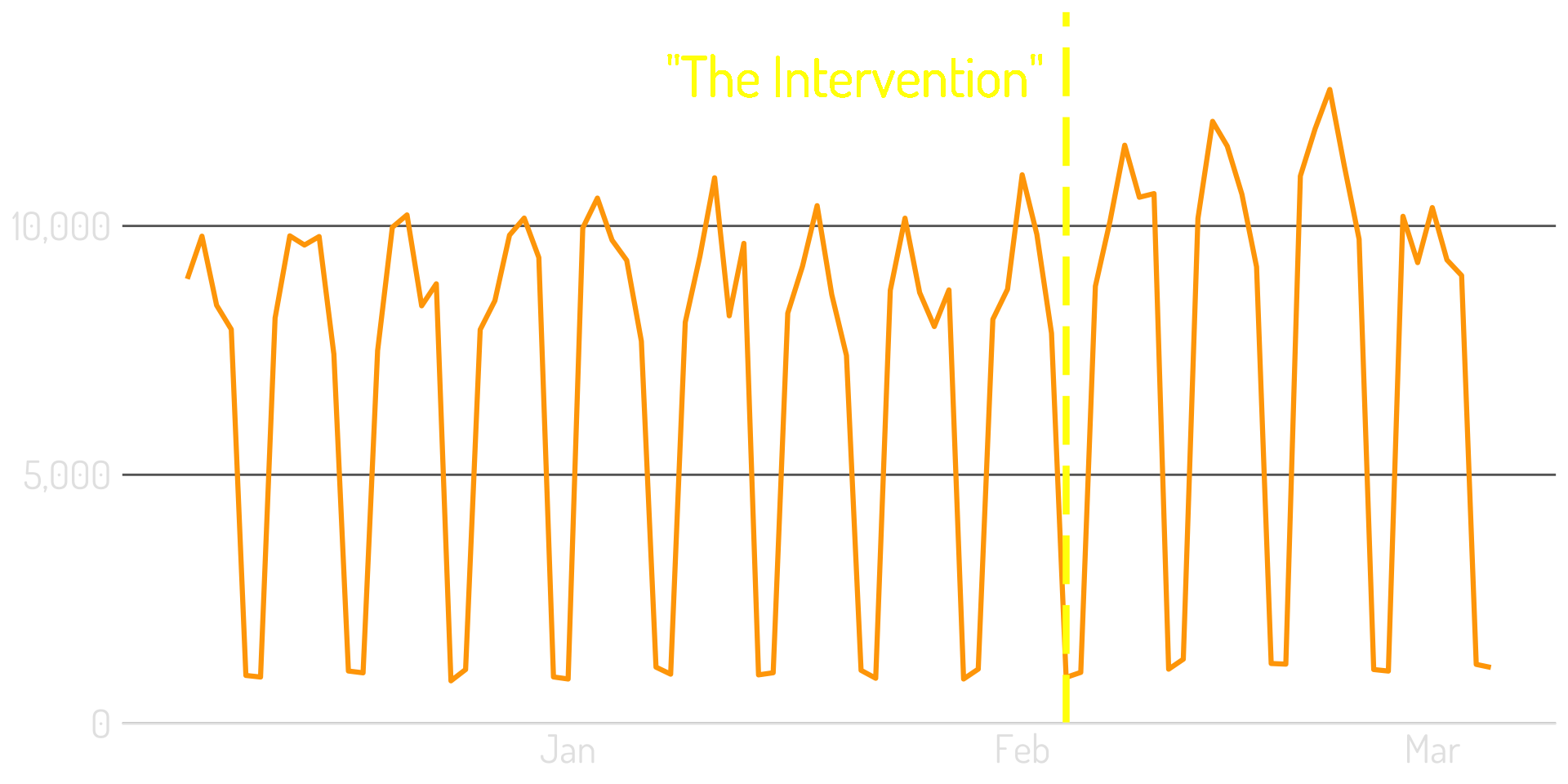
CausalImpact uses historical data to forecast what’s expected
Step 1: Look at the pre-intervention data
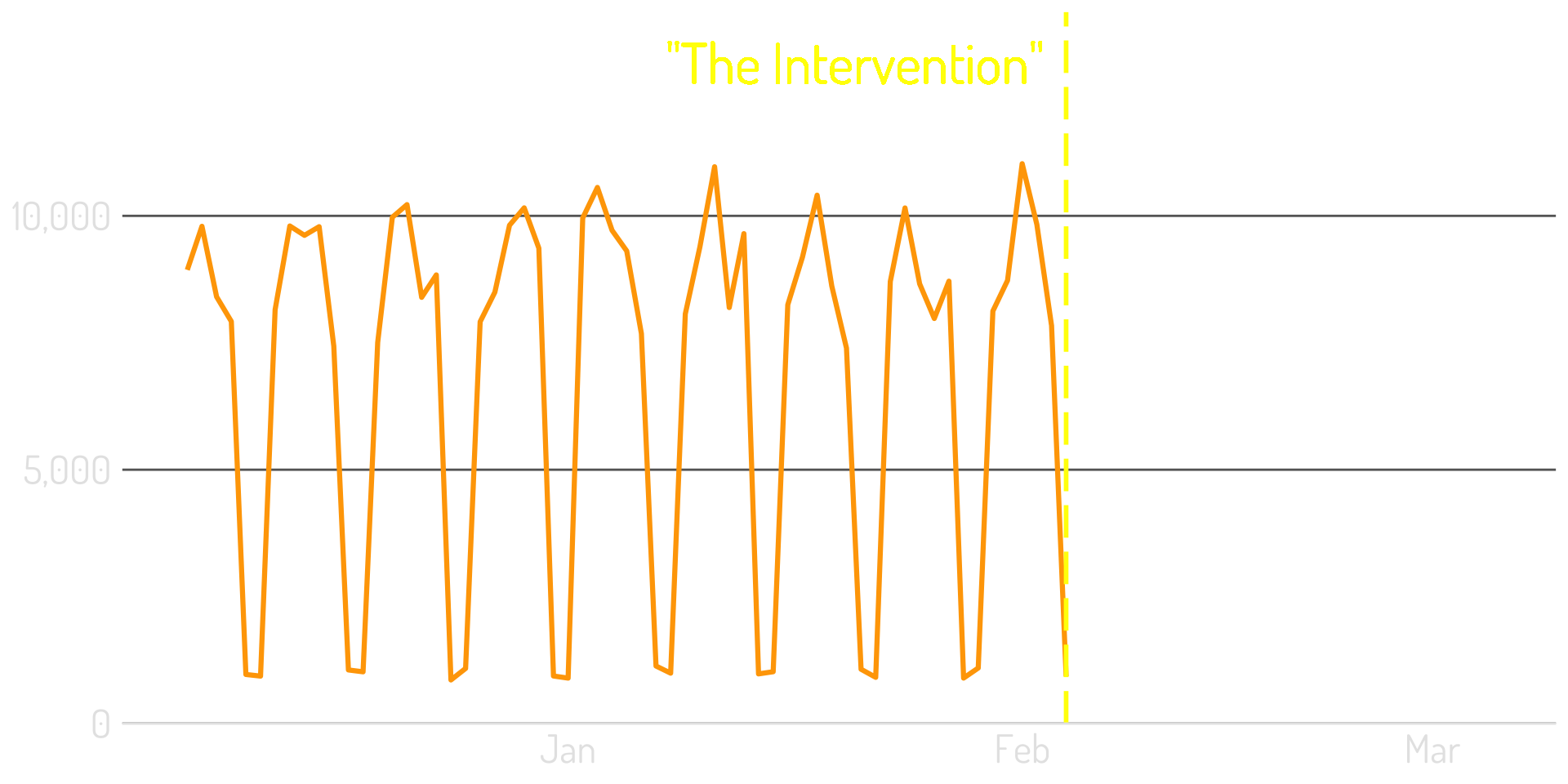
Step 2: Build a best-fit model using this data
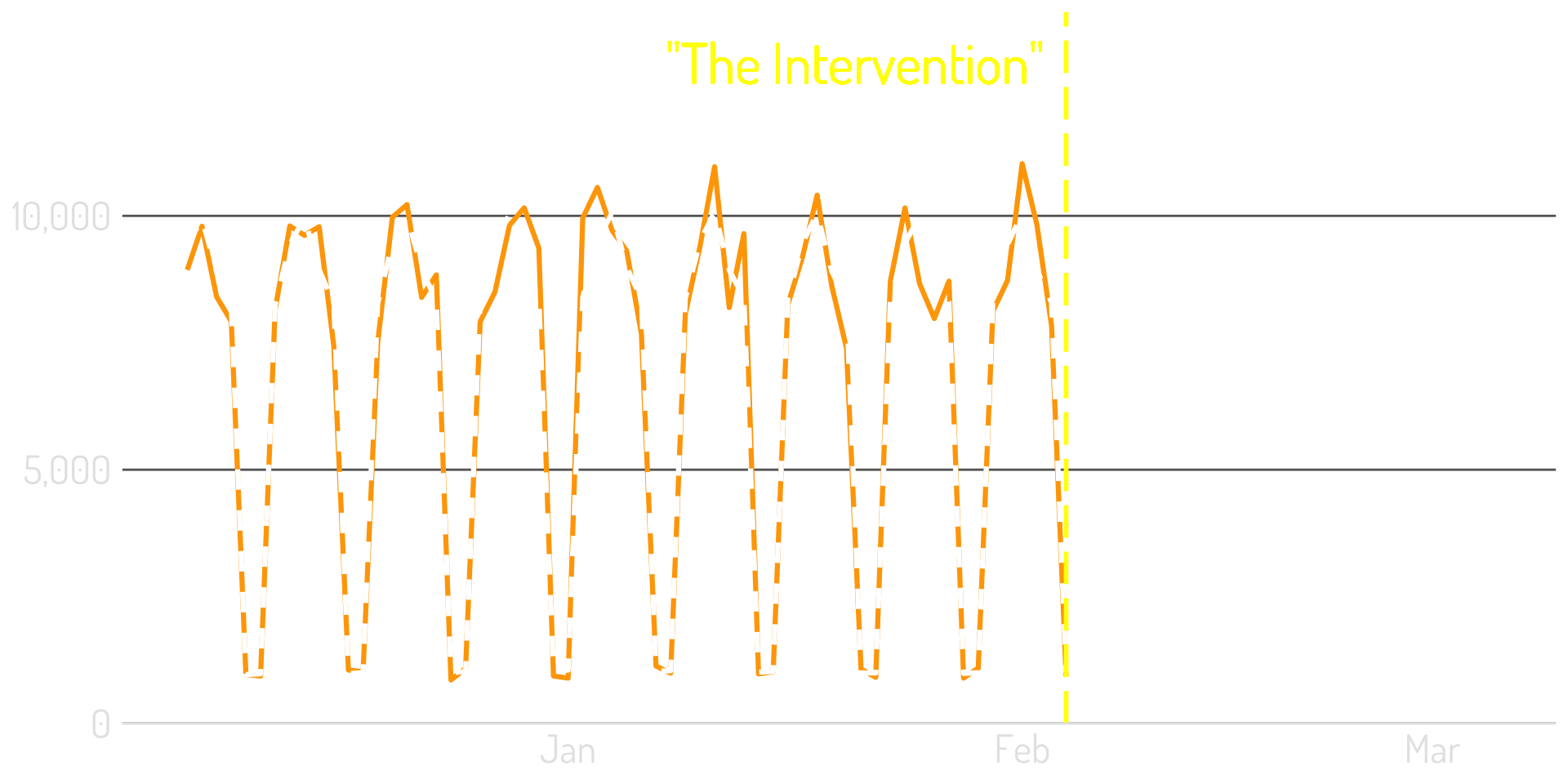
Step 3: That model can quantify its uncertainty
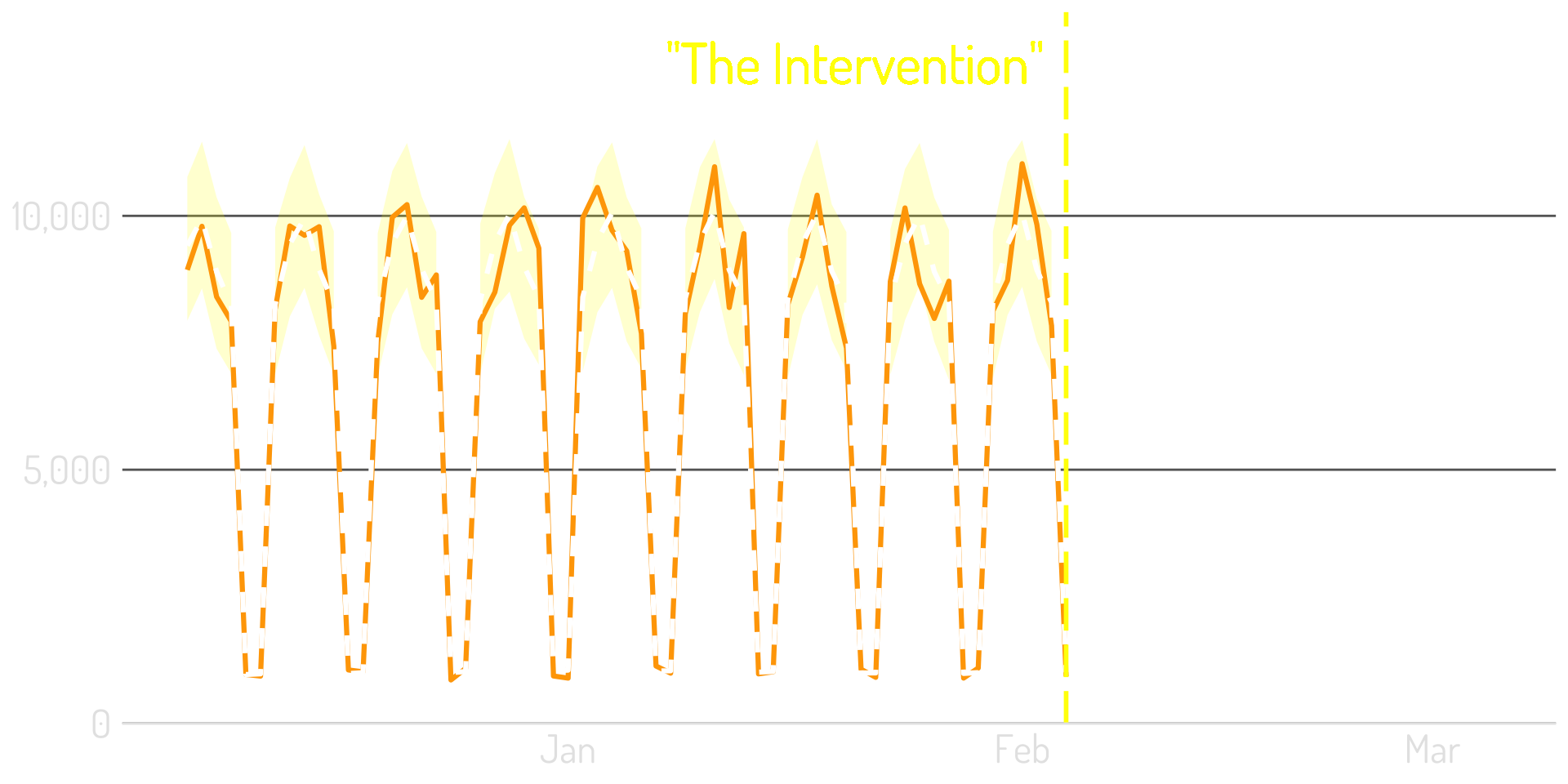
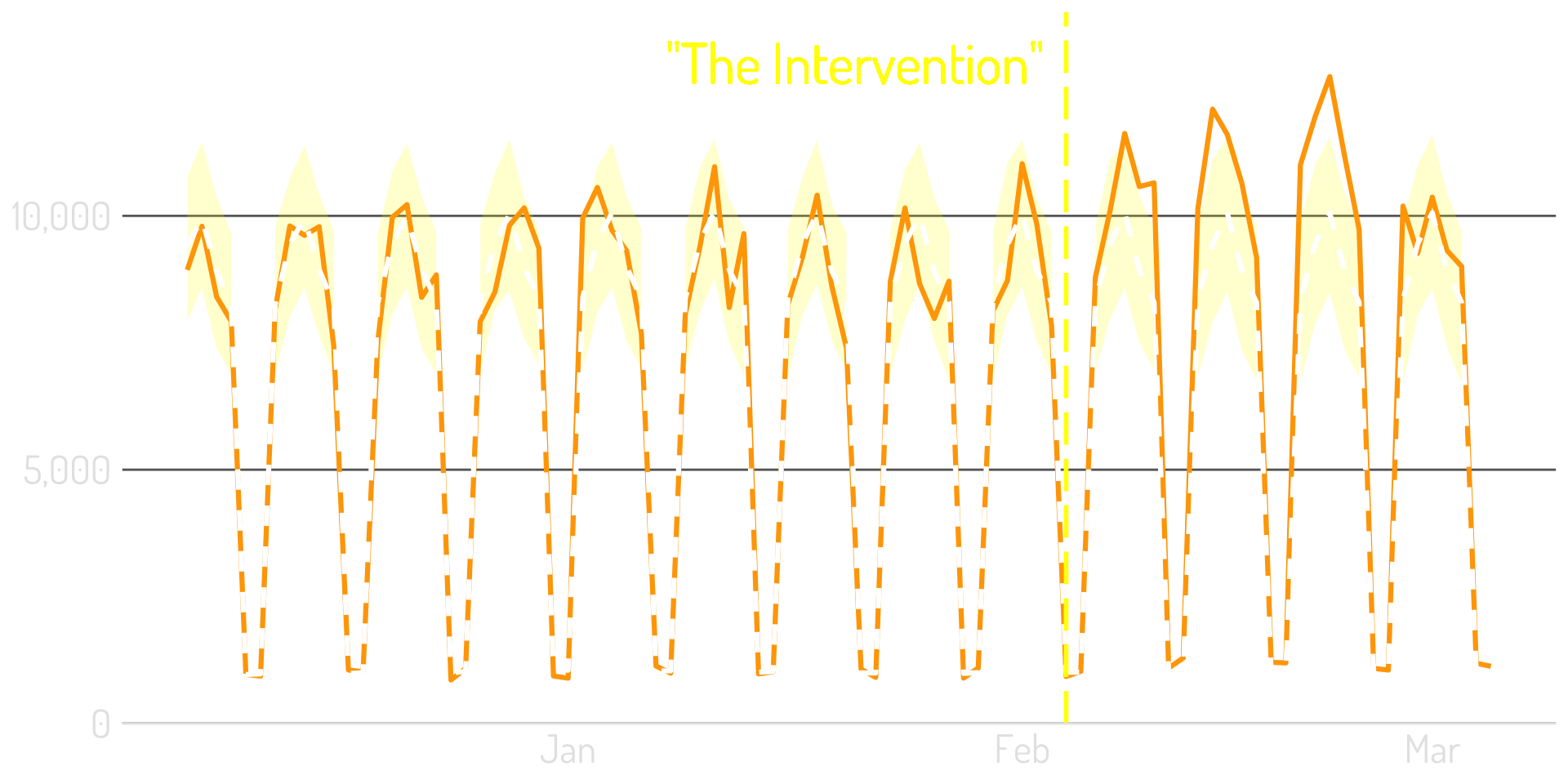
Step 4: Extend the model post-intervention
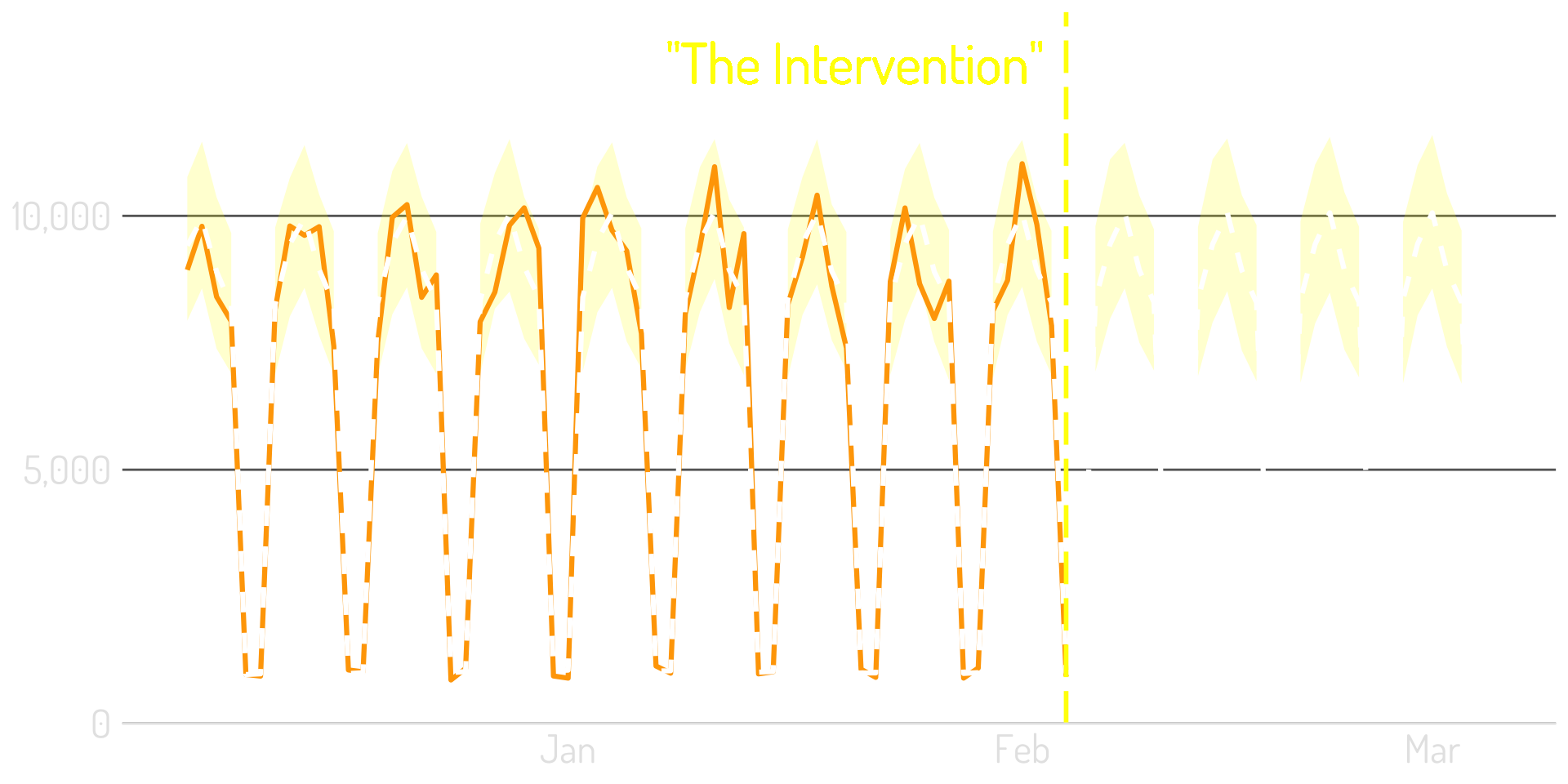
Step 5: Compare the model to the actual results
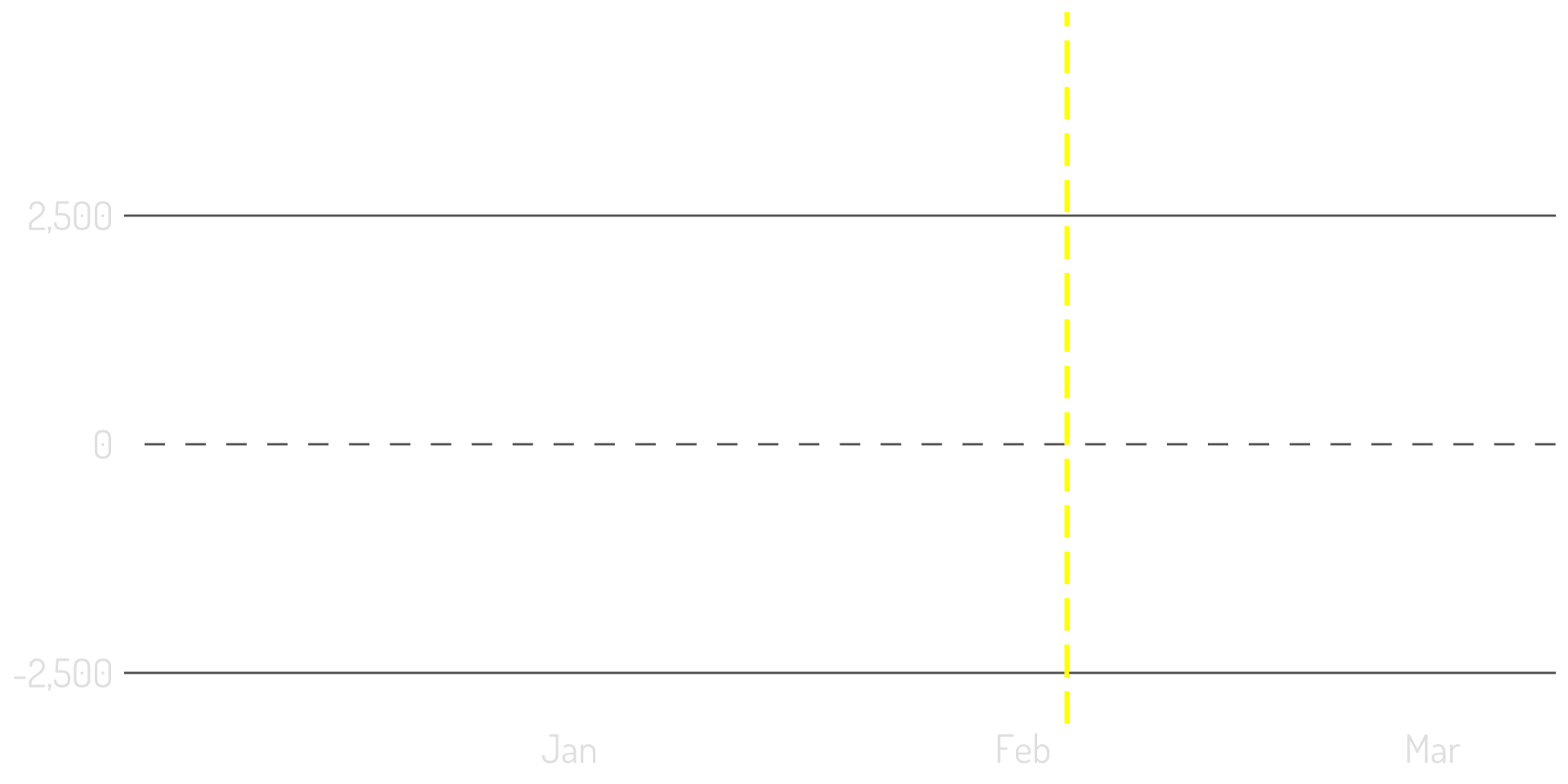
“Pointwise” is another way to look at the results
Set the modeled prediction as the baseline
Plot the difference between the model & the actual
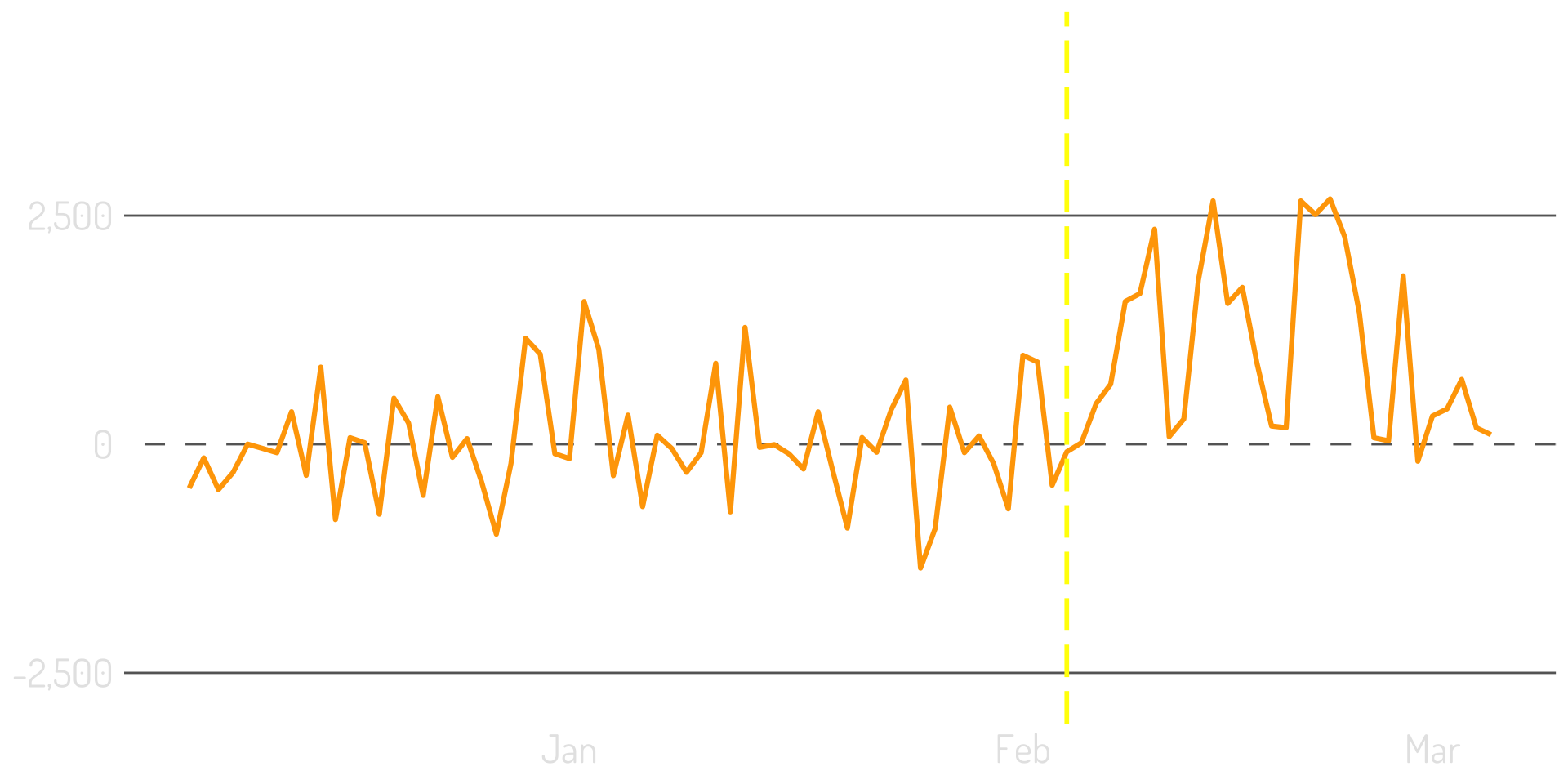
Put the confidence interval around the difference
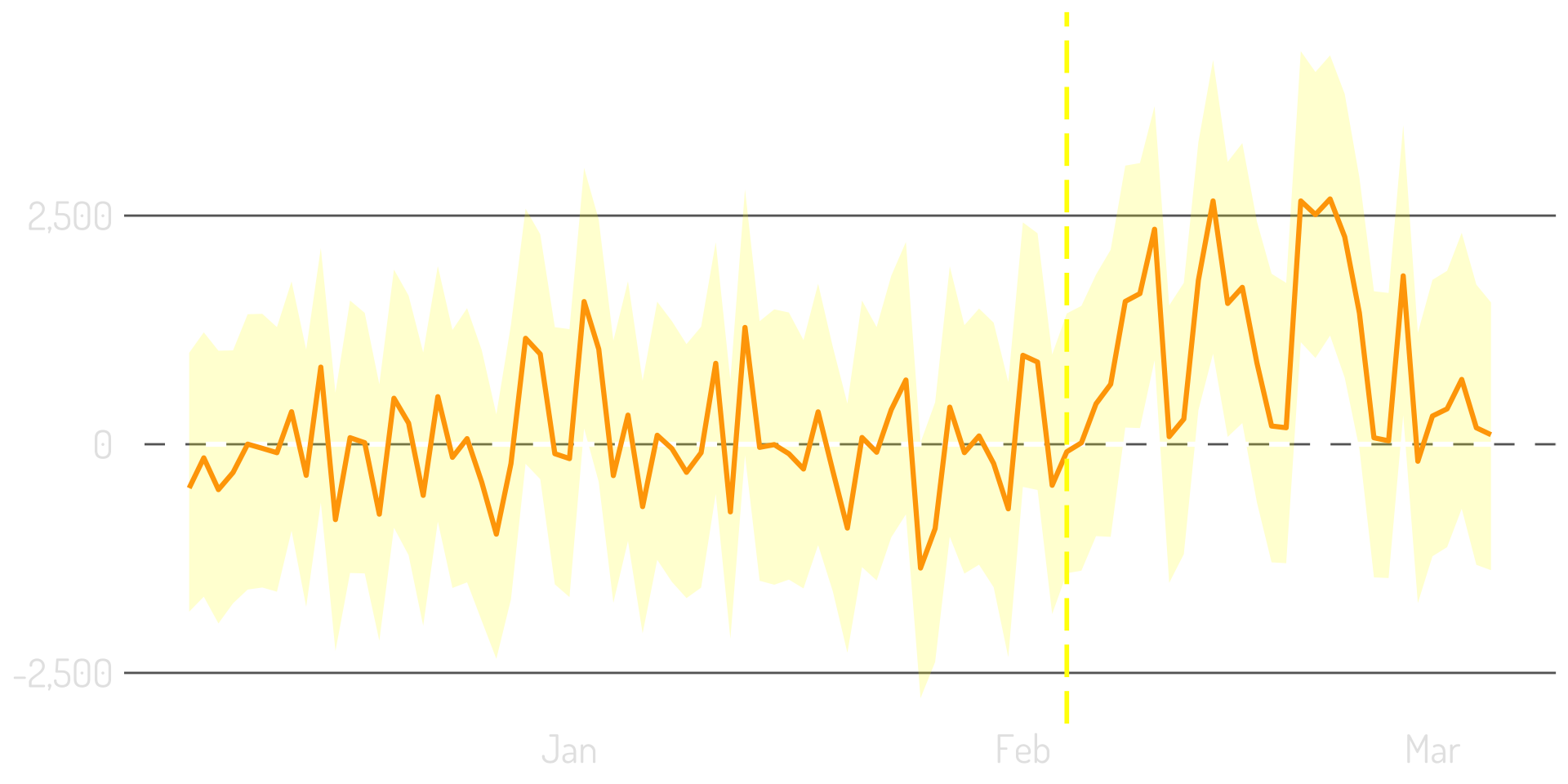
Or…by the numbers!
Posterior tail-area probability p: 0.0010549
Estimated average (daily) effect: 1,032 with a 95% confidence interval of 580 to 1,495
But, wait! There’s more!
Putting covariates to use
Their relationship to the metric of interest is stable
They are not themselves affected by the intervention

This is not a silver bullet!

Let’s review!
What is “the population?”
Regardless…“the sample” is not ideal
Stationarity: constant mean, constant variance
First differences: don’t jump to correlations
Time-series decomposition
Bayesian structural time-series


Time…is hard.

Thank you!
Presentation: bit.ly/sw-time-series
Podcast: analyticshour.io
LinkedIn:

 This presentation was 100% built with R (and Quarto w/ reveal.js)
This presentation was 100% built with R (and Quarto w/ reveal.js)
 The images are (almost) 100% DALL-E 2
The images are (almost) 100% DALL-E 2
 The background image is from my “daily diversion” on Twitter
The background image is from my “daily diversion” on Twitter
bit.ly/sw-time-series | @tgwilson | tim@gilliganondata.com